
News
Jackpot King Games are the Latest Innovation in an Evolving Slots Market
The slots market has undergone many developments over the last few years, with a notable influx of new game mechanics. …
News, Technology
The SODEXO Reward Hub Login at sodexorewardhub.com

News, Technology
USPayserv Login – Pay Stubs & Electronic Payroll Services Guide
Education, Technology
Myhr Mizzou Login At Myhr.umsystem.edu

News, Technology
LMPeople Login – LMPeople Employee Sign in at www.lmpeople.com

Jackpot King Games are the Latest Innovation in an Evolving Slots Market
Akshay Varma
The slots market has undergone many developments over the last few years, with a notable …
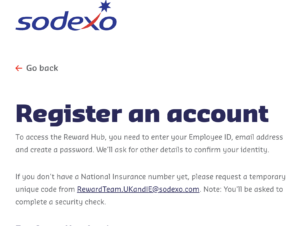
The SODEXO Reward Hub Login at sodexorewardhub.com
Akshay Varma
Sodexo Reward Hub is a digital platform that provides a comprehensive and flexible solution for …

USPayserv Login – Pay Stubs & Electronic Payroll Services Guide
Ilina Singh
USPayserv, a component of the USVerify HR outsourcing suite of applications, is an electronic distribution …
Myhr Mizzou Login At Myhr.umsystem.edu
Bryan Lucifer
Mizzou, or the University of Missouri, is one of the most reputed public research universities …

MyGroundBiz Login – Steps To Access Your Account at www.Mygroundbiz.com
Aparna P Raj
MyGroundBiz is an online portal designed by FedEx for its users. The registered users are …

Jackpot King Games are the Latest Innovation in an Evolving Slots Market
The slots market has undergone many developments over the last few years, with a notable …
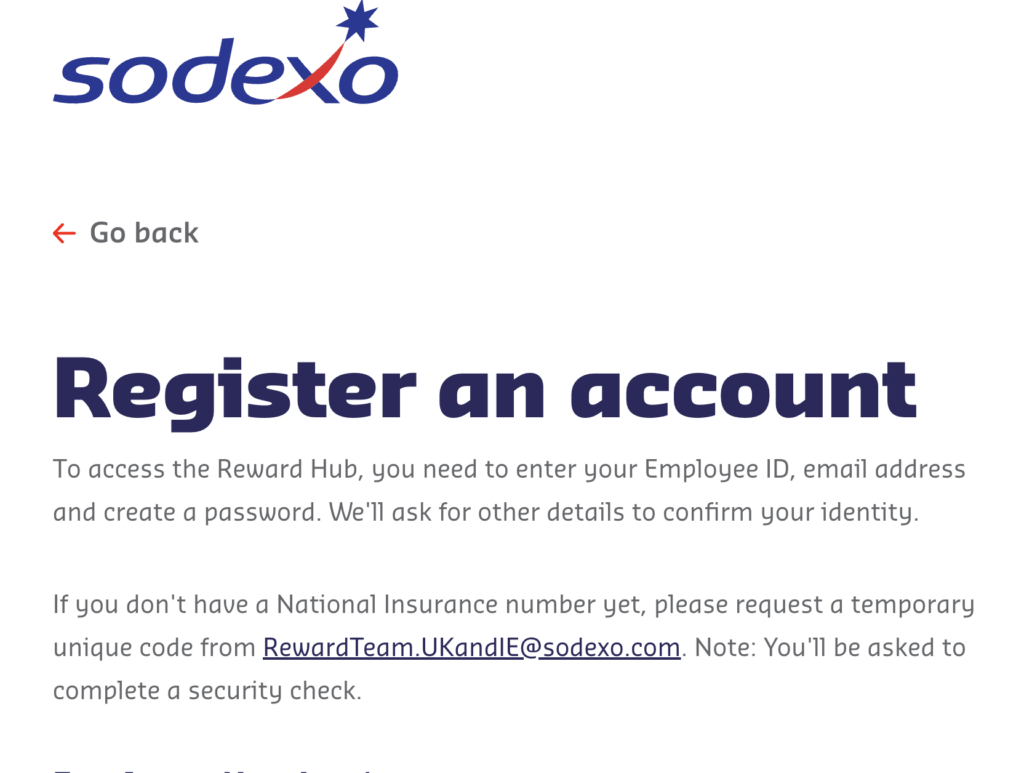
The SODEXO Reward Hub Login at sodexorewardhub.com
Sodexo Reward Hub is a digital platform that provides a comprehensive and flexible solution for …


